The Solar Surface

The Sun is a dynamic star. Galileo first identified sunspots and limb darkening on the solar surface. The discovery of sunspots refuted the idea that they were objects transiting in front of the Sun, but rather part of the surface of the Sun itself, whilst the limb darkening demonstrates that the Sun is a gaseous body surrounded by a photosphere. H-alpha imaging (which detects the Balmer 3-2 transition of Hydrogen) is a powerful means to peer into the solar chromosphere, the layer directly above the photosphere, picking out flares and prominences.

The Sun also has variability, on timescales of a few hours due to magnetic phenomena on the surface, to (many) years, in particular the 11-year cycle which appears to arise from the complicated magnetic phenomena. Observation of the changing nature of the solar surface date back to the 17thcentury, and now, space-based measurements show that the luminosity varies by 0.1% over the solar cycle (e.g. Pap et al. 2003). The link between solar activity, total stellar irradiance has led to a deeper understanding of the solar physics, and for a debate on the role of the Sun in Earth's climate.

The goal of this project is to measure the properties of the Solar photosphere and chromosphere (using Halpha filters). There are two possible science projects. You can undertake one, or both projects.

1. The Properties of Sun Spots, prominences and the Solar surface

The sun rotates faster at the equator, causing the magnetic field lines to become stretched by differential rotation. Over time the magnetic field lines can form loops and break the surface of the photosphere. This is when sunspots are most likely to occur.

A sunspot is a dark region that appears on the photosphere namely the Sun’s 'surface'. The planet-size regions are darker because they are much cooler than their surroundinging. The lower temperatures are due to convection being inhibited by the strong magnetic activity reducing the transport of energy from the interior to the surface.

The solar surface is also remarkably active, with "features" that can be as small as 30km across (e.g. see the recent article using Solar observations from Hawaii). With the fast camera, it may also be possible to image some of the granulation on the surface of the Sun.

Here are some suggestions for objective you may wish to consider.

  1. Familiarise yourself with the telescope, camera and solar filters.

  2. In the lab, take a set of images, and become familiar with how and where the data is stored. The fast camera will write the images to the data archive. You will need to check the linearity of the camera by taking some images of a flat-field.

  3. Using the telescope, solar filter and camera take a series of images of the Sun. You may want to take a number of images at different exposure times and filters. The cameras include U, B, V, R and I broad-band filters, and also a H-alpha narrow-band filter.

  4. Identify the best observation(s) and analyse them to identify the sun spots (broad band images) and prominences (Halpha), and test whether the granulation can be detected. If necessary, calibrate the images from counts to flux using the calibration curves. You may also need to take flat fields.

  5. Over the course of a few days, count the Sun spots, and measure how the prominences evolve. Is the number of Sun spots consistent with the current point of the Solar cycle? Is it possible to follow the prominences in Halpha in real time?

  6. By comparing the Sun spot intensity to the surrounding surface intensity, derive the temperature of the Sun spots. Are the Sunspots resolved (i.e. can you measure their physical size?)

  7. Over the course of a few weeks, can you measure the (differential) rotation speed of the Sun?

  8. The "fast" camera can take images 1000's of images per second. This means that it should be able to "lucky" images. Is it possible to dected/resolve granulation on the solar surface?

2. Measuring the Limb Darkening

Solar images in the visible wavelength range show that the disk centre is brighter than the limb region. This phenomenon is known as the 'limb darkening'. Photons that originate from the nuclear fusion processes in the core of the Sun are scattered and absorbed on their random walk to the surface of the star, driven by the decreasing pressure and temperature gradient. This creates sources of opacity, which inhibit the radiative transfer of energy. The optical depth describes the number of mean free paths (distance travelled without any scattering or absorption events) the photon must travel through to reach the stellar surface.

When we image solar disk, the center is dominated by radiation which is coming radially outwards. These photons originate relatively deep in the photosphere, where the temperature is relatively high. At the limb (edge) of the Sun, the radiation has skimmed through the photosphere at a shallow angle. These photons originate in the upper reaches of the photosphere, where the temperature is lower. This gives rise to the effect of the limb darkening.

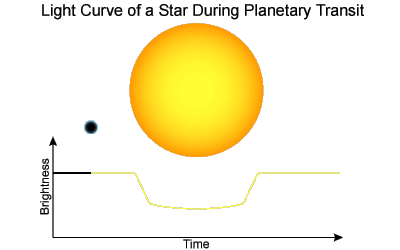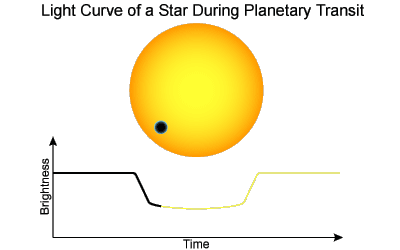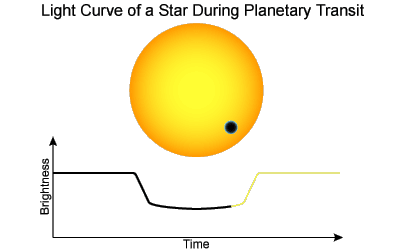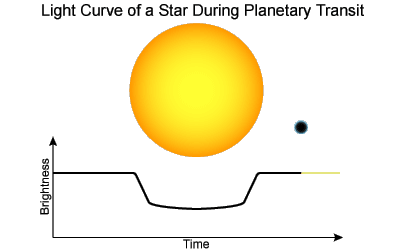
The (wavelength dependent) limb darkening is interesting to study in its own right, but has more far reaching consequences. In particular, space based observatories, such as Kepler have identified thousands of planets through the transit method, in which a planet that passes infront of a star ecclipses a (very small) fraction of the light. The depth and shape of the light curve reflect a number of factors, including the limb darkening, ratio of size (radius) of the star to planet, and the orbital parameters.

The simplest form of the limb darkening can be described in terms of the specific intensity I originating from the stellar core. In the Eddington approximation, the intensity as a function of radius can be described by:

where the left hand side of the equation is the normalised intensity, and u is the (wavelength dependent) limb darkening coefficient. Additional quadratic and Claret 4-parameter laws are also applicable if high-enough quality data can be derived.

In this project, the aim is to measure the limb darkening of the Sun, and then to test the effect that the limb darkening should have on an exoplanet transit light curve obtained from (i) a telescope in Durham, and (ii) the Kepler space telescope. The goals of the experiment can include:

  1. Familiarise yourself with the telescope, camera and solar filter.

  2. In the lab, take a set of images, and become familiar with how and where the data is stored. The camera will write the images to the archive. Check whether the conversion from photons to counts is linear. You may need to construct a set of calibration curves to convert counts to flux using observations in the lab.

  3. Using the telescope, solar filter and camera take a series of images of the Sun. You may wish to take images in different filters, and the camera includes U, B, V, R, I and Halpha filters.

  4. Identify the best observation(s) and analyse them to extract the intensity as a function of radius (time permitting, in different filters). If necessary, calibrate the images using the linearity curve.

  5. Measure the limb darkening coefficient (as a function of wavelength). This could first be done numerically, but also try a functional fit to the data. How many parameters are needed to fit the data?

  6. With the limb darkening measured, identify a star which has a known exoplanet with the same colours as the Sun, and preferably that has been observed from Durham (matching the colours should result in a similar limb darkening curve as the Sun). Measure the light curve from archival observations, and use the limb darkening curve to correct the observations. Is the correction significant given the signal-to-noise of the data. Repeat this experiment for the same observations from Kepler (where the S/N is much higher). What is the effect of the limb darkening on the derived properties of an exoplanet?

Back to the AstroLab Home Page ams 2019-Feb-09 13:28:13 UTC