This Page
› Halos and Subhalos › ID numbers › Structure of the merger trees › Format of the tree files

Halos and subhalos

The merger trees are built using the Friends of Friends (b=0.2) groups output by L-Gadget2 and the subgroups identified by SubFind. In the description below 'subhalo' means a set of particles grouped together by SubFind, which looks for gravitationally bound local density maxima. A 'halo' is a collection of subhalos grouped together in the following way:

Initially subhalos are grouped into halos by looking at the FoF groups - a halo just consists of all the subhalos belonging to one FoF group. Particles in the FoF group which do not belong to any subhalo are discarded. Note that SubFind identifies the background mass distribution of the halo as a subhalo, so each halo will normally contain one large subhalo (with most of the mass of the halo) and a set of smaller "satellite" subhalos.

The Friends of Friends algorithm often links together objects which should probably be treated as separate halos as far as the merger trees are concerned. So under certain conditions a subgroup may be split from its parent halo and considered to be a halo in its own right. This is done if 1) the subhalo is outside twice the half mass radius of the parent halo or 2) the subhalo has retained 75% of the mass it had at the last output time where it was an independant halo. This second condition is based on the assumption that a halo which has fallen into a more massive halo will rapidly be stripped of its outer layers, whereas a halo which has been artificially linked to another halo will retain its mass. When a subhalo is split off, any less massive subhalos within twice its half mass radius are also split off and become part of the new halo.

One side effect of this splitting algorithm is that the halos used in the construction of the merger trees are NOT just Friends of Friends groups. The number of halos after splitting is slightly greater than the number of Friends of Friends groups.

ID numbers

At a given output time each subhalo has a unique ID number. These numbers are assigned in the order the subhalos appear in the SubFind output files, starting from one. All of the subhalos in file 0 are assigned ID numbers first, then those in file 1, then those in file 2 and so on up to file 511, so that the maximum subhalo ID at any output time is equal to the total number of subhalos identified at that time. Halo IDs are assigned in the same way. These numbers are used to specify the descendant of each halo/subhalo in the merger tree.

Structure of the merger trees

One merger tree is generated for each halo which exists at the final output time of the Millennium simulation (snapshot number 063). The merger tree contains information about all of the progenitors of the halo at all earlier snapshots, including a list of the subhalos in each progenitor halo and the final halo. The diagram below shows part of a possible merger tree - only the last four output times are shown:

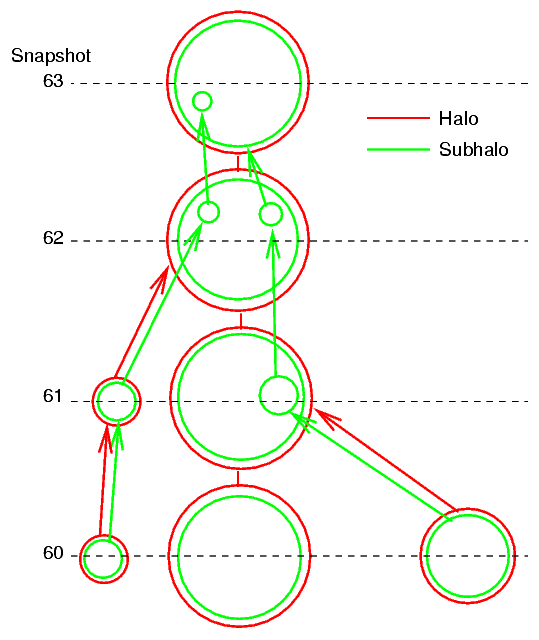
Merger tree diagram

The final halo is shown at the top with time increasing up the page. Halo mergers occur between snapshots 60-61 and 61-62, although the smaller halo in each case survives as a subhalo in the descendant halo. Between snapshots 62 and 63 one of these subhalos ceases to be identifiable as a separate object - it merges onto the main subhalo (ie the background mass distribution) of its parent halo. The other subhalo survives until the final output. Note that a halo may contain subhalos which cannot be traced back to a progenitor halo. The merger trees contain information about ALL the subhalos identified in each halo.

The descendant of a subhalo is found by following the most bound 10% of its mass or the 10 most bound particles, whichever is the greater mass. The descendant is the subhalo which contains the largest number of these particles. The descendant subhalo will usually be at the next output time, but this is not always the case. If a subhalo cannot be identified as a separate object in the next snapshot it may be possible to locate it at a later time. The merger tree building code attempts to match these subhalos to 'orphan' subhalos at any of the next five output times. Orphan subhalos are subhalos with no progenitors in the previous snapshot.

The descendant of a halo is the halo which contains the descendant of the most massive subhalo in the halo.

Format of the tree files

The merger trees are stored in
/data/rw1/jch/trees/treedir_063/splittrees_063.*
There are 512 (Fortran unformatted) files. Each tree file starts with a header which can be read in with something like 
READ(1) ntrees, ifirstsnap, ilastsnap               ! All INTEGER*4
READ(1) redshift(ifirstsnap:ilastsnap)              ! A REAL*4 array
The number of merger trees in this file is given by ntrees. ifirstsnap and ilastsnap give the indices of the first and last snapshots used in the construction of the merger trees - the final halos exist at snapshot ilastsnap and progenitors may exist at snapshots between isnapfirst and isnaplast. The redshifts of the snapshots are stored in the redshift array.

The merger trees are then stored in sequence. Each one can be read with 
READ(1) ifirst, ilast, nhalo, nsubhalo              ! All INTEGER*4
READ(1) nhalostep(ifirst:ilast)                     ! An INTEGER*4 array
READ(1) id,np,idesc,halodecstep,nsphalo,firstsub
READ(1) subid,subnp,subidesc,subdecstep,pos,vel,veldisp,vmax,spin,mostboundid,rhalf
where the types of the data arrays are
INTEGER*4, DIMENSION(nhalo)    :: id, np, idesc, halodecstep, nsphalo, firstsub
INTEGER*4, DIMENSION(nsubhalo) :: subid,subnp,subidesc,subdecstep
REAL*4, DIMENSION(3,nsubhalo)  :: pos, vel, spin
REAL*4, DIMENSION(nsubhalo)    :: veldisp, vmax, rhalf
INTEGER*8, DIMENSION(nsubhalo) :: mostboundid
(in practice these arrays will need to be dynamically allocated as each tree is read)

The array nhalostep gives the number of halos in the tree at each snapshot. The integers ifirst and ilast give the first and last snapshots where there are any halos in the merger tree. ilast should always be 63, since there must always be a halo at the final time. For low mass final halos ifirst can be quite close to ilast because the halo may have formed recently.

For each halo in the tree the following information is available:
The information stored for each subhalo is:
The subhalos in a given halo can be found using the firstsub and nsphalo arrays. All of the subhalos in a given halo are stored consecutively, so the following loop would print out the particle numbers and positions of all of the subhalos in halo ihalo:
DO isub = firstsub(ihalo),firstsub(ihalo)+nsphalo(ihalo)-1,1
 WRITE(*,*)subnp(isub),pos(1,isub),pos(2,isub),pos(3,isub)
END DO
Halos and subhalos are stored in order of the snapshot they exist at, earliest first. Halos and subhalo which exist in the same snapshot are stored consecutively so the nhalostep array can be used to find all the halos in the tree at a given snapshot. To loop over all halos at snapshot isnap and write out their IDs and masses for example:
istart  = SUM(nhalostep(ifirst:isnap - 1)) + 1
ifinish = istart + nhalostep(isnap) - 1
DO ihalo = istart, ifinish, 1
  WRITE(*,*)id(ihalo),np(ihalo)
END DO
To locate the descendant of a halo ihalo it is neccesary to find the halo jhalo at snapshot halodecstep(ihalo) such that idesc(ihalo) = id(jhalo). Subhalo descendants may be found in the same way.