 |
Department of Physics | User's Guide to the Night Sky |
The Ecliptic: the Sun's Annual Path on the Celestial Sphere
As the Earth orbits around the Sun over the course of the year, we observe the Sun to track out a circle around the celestial sphere. This track of the Sun on the celestial sphere is called the ecliptic. Relative to the "fixed" stars we observe the Sun to move eastwards on the celestial sphere completing one full circuit of 360° over the year (~365.25 days), i.e. an eastward motion of ~1° per day. The zodiac is the set of constellations on the ecliptic, (i.e. those that the Sun travels through in the course of the year). The traditional twelve zodiac constellations are Aries, Taurus, Gemini, Cancer, Leo, Virgo, Libra, Scorpio, Sagittarius, Capricornus, Aquarius and Pisces.
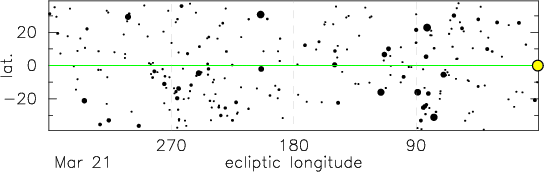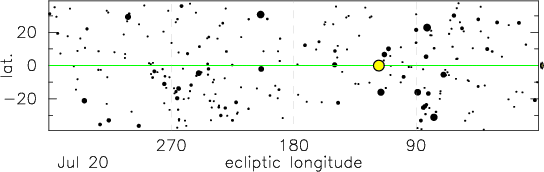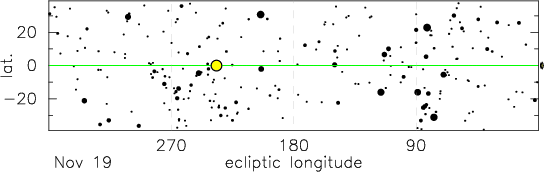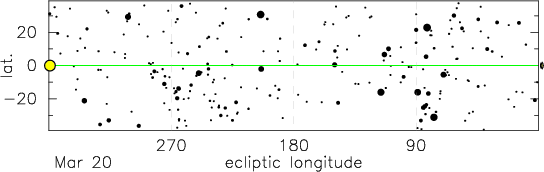
The animation above shows the Sun moving along the ecliptic (green line) over the course of one year. This diagram is in ecliptic coordinates, i.e. relatively to ecliptic (longitude measures the angle around the ecliptic and latitude measures the angle away from the ecliptic). By definition the Sun tracks along the zero ecliptic latitude line.
The Earth's spin axis is tilted by 23.5° with respect to the Earth's orbital plane (the ecliptic plane). The direction of Earth's spin axis is fixed in space.
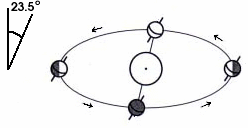
The tilt of the Earth's spin axis with respect to the ecliptic plane results in the Sun tracking out an seemingly sinusoidal path on the celestial sphere when viewed in the projection with the celestial equator horizontal.
The animation above shows the Sun moving along the ecliptic (green line). This diagram is in equatorial coordinates, i.e. Right Ascension and Declination. The (red line) is the celestial equator. In the course of the year, the Sun spends six months above the celestial equator (~21st March to ~20th September) and six months below (~20th September to the ~21st March). It is this 23.5° tilt of the Earth's spin axis with respect to the ecliptic plane which causes the seasons.
Each year we see the Sun cross the celestial equator moving northwards on about 21st March. This is the vernal (March) equinox and at this time the Sun, by definition, is at RA = 0h, Dec = 0.0°. At the equinoxes at every location on the Earth the Sun spends 12 hours above the horizon and 12 hours below the horizon. The Sun rises precisely in the East and sets precisely in the West; the Sun is on the celestial equator. This animation shows the track of the Sun across the sky as seen from Durham at the time of the equinox.
For northern hemisphere observers the Sun stops moving up the celestial sphere reaching its highest point on about 21st June, i.e. at the summer (June) solstice. The word solstice means "Sun standing still". At this time the Sun is at RA = 6h, Dec = +23.5°. At this time northern hemisphere observers receive the maximum amount of sunlight because the Sun is highest in the sky at noon and is above the horizon for the longest period. This animation shows the track of the Sun across the sky as seen from Durham at the time of the summer solstice.
On about 20th September, the Sun crosses the celestial equator moving southwards. This is the autumnal (September) equinox. At this time the Sun is at RA = 12h, Dec = 0.0°.
The Sun reaches its lowest point at the winter (December) solstice on about 21st December. At this time the Sun is at RA = 18h, Dec = −23.5°. Northern hemisphere observers receive the minimum amount of sunlight at this time as the Sun is lowest in the sky at noon and is above the horizon for the shortest time. This animation shows the track of the Sun across the sky as seen from Durham at the time of the winter solstice.
This animation shows how the position of the midday Sun changes over the year as seen from Durham.
A good approximation to the Sun's position
is given by
RA [deg] = λ + 2.45 sin 2λ
sin Dec [deg] = 0.4 × sin λ
( or Dec [deg] = 23.5 × sin λ ) ,
where λ is the Sun's ecliptic longitude.
λ can be estimated by assuming that the Earth's orbit is circular
( λ = 0° on 21st March,
λ = 30° on 21st April,
λ = 60° on 21st May,
λ = 90° on 21st June,
etc). For example, estimate the Sun's RA and Dec on 21th January?
At this date the Sun's λ = 300° (i.e. about two months
before the vernal equinox). Using the above formulae we estimate that on the 21st
January the Sun's RA = 299.1° (19h 56.4m) and Dec = −20.3°.
| User's Page | ams |