Various analysis of subsets of these N-body simulations have been published. The abundance and evolution of galaxy clusters was studied in Eke etal (1996) . The properties of COBE normalized CDM models was discussed in Cole etal (1997) . Hatton and Cole (1997) used the simulations to investigate the redshift space distortion of galaxy clustering.
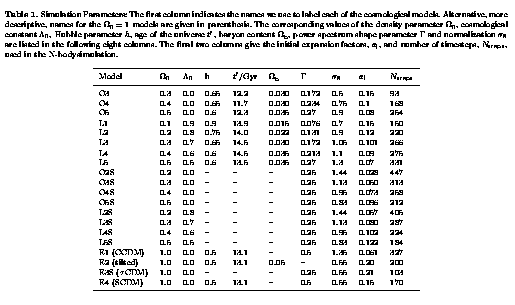
Each of the simulations was of a periodic box of side 345.6 Mpc/h (192x1.8 Mpc/h). For each, we created a Gaussian random density field on a 192^3 grid, using the same Fourier phases from one model to the next, but varying the mode amplitudes according to the model power spectrum. We applied the Zel'dovich approximation to this density field to compute displacements and peculiar velocities at each grid point. We then displaced each particle from its starting position in a ``glass'' configuration according to the displacements interpolated from the grid values. The initial expansion factors of the simulations listed in the following table, were determined by setting the amplitude of the initial power spectrum at the Nyquist frequency of the particle grid to be 0.3^2 times that for an equivalent Poisson distribution of particles.
We evolved the simulations using a modified version of Hugh Couchman's Adaptive Particle-Particle-Particle-Mesh (AP^3M) N-body code. We set the softening parameter of AP^3M's triangular-shaped cloud force law to 270 kpc/h, 15% of the grid spacing. Thus the softening scale is fixed in comoving co-ordinates. This choice corresponds approximately to a gravitational softening length 90 kpc/h for a Plummer force law. The size of the time step was chosen so that the following two constraints were satisfied throughout the evolution of the particle distribution. First, the rms displacement of particles in one timestep was less than eta/4. Second, the fastest moving particle moved less than eta in one timestep. Initially these two constraints are comparable, but at late times the latter constraint is more stringent, particularly in low $\Omega_0$ simulations. We monitored energy conservation using the Layzer-Irvine equation and found that for this choice of timestep energy conservation with a fractional accuracy of better than 0.3% was achieved. We also tested the inaccuracy incurred by these choices of starting amplitude and timestep by comparing the final particle positions with two additional versions of an Omega_0=1 simulation that were run starting from a fluctuation amplitude a factor of two lower and using timesteps a factor of two smaller. In each case we found that the final particle positions agree very accurately, with rms differences of less than 270 kpc/h More importantly, the correlation functions of each particle distribution were indistinguishable at scales larger than 90 kpc/h. Thus the statistical clustering properties of these simulations have their resolution limited by the particle mass and force softening and not by the choice of timestep or starting redshift.